您所在的位置：什锦文坊 >> 世界之最 >> 正文

世界上最小的家具:仅指甲盖大小(完全使用榫卯结构)

2024-04-10 20:00:16 来源：网络整理作者：管理员

世界上最小的家具

阎明怡的本职工作是武汉冶金设备制造公司的一名员工，他从1999年做出首个微型的可使用的明式家具之后就一直在不断的继续创作，到现在已经制作了超过50个非常具有特点的明式家具，大多是使用和实物一样的木材，比如黄花梨、紫檀木等最值钱的树木材料，打磨的非常光滑细腻，看起来也同样和实物一样带有漂亮的纹理。

在这50件明式家具中不仅有手掌大小的太师椅、卧榻、八仙桌，还有指甲盖大的木刨工具、斧头以及方形锯等，其中作为工具的微型家具则全部都是能够使用的，比如木刨可以刨木花，而锯子则可以锯断细小的枝条，而其他的座椅等家具则是由榫卯进行拼接的，几乎可以说完全的还原了真实的家具功能。

阎明怡虽说并不是行家出身，但据他表示自己非常喜欢做木工，之所以会想要做出一套完美的明式家具，是因为偶然的在杂志上看到了它们，并且意外的发现了这些明式家具的魅力，明式家具的特点就是以简洁为主，但简洁的恰到好处，没有使用任何一根钉子，几乎可以说明朝是将榫卯工艺发挥到极致的一个巅峰时代。

而就是这样精美且具有特殊价值的明式家具，现在却已经越来越少，只有1千多件，因此阎明怡变开始想要将一些这些明式家具留下，因为很多人都不了解这种家具，以至于他看到不少的人都将它们砍成木材或者卖给了外国人，因此他变想要以这种微型家具的方式来保留并且宣传明式家具，因此菜创造出了世界上最小的家具。

显示全文

上一篇：世界上最无聊的三大发明:没有灵魂的自动撸猫器

下一篇：世界上速度最快的飞机速度令人难以想象（7274km/h）

为您推荐

电报的发明者是谁电报出现在什么时候是谁发明的

电报的发明者是塞缪尔·莫尔斯。莫尔斯原本的职业并不是科学家，而是一位画家，之所以会产生发明电报的想法，是因为杰尔逊医生对莫尔斯说，无论电线有多长，电流都能迅速通过，这句话让莫尔斯对电流产生了兴趣，从此便踏上了发明电报的道路。...

发布时间：2024-04-10 21:00:07

世界上最小的家具:仅指甲盖大小(完全使用榫卯结构)

世界上最小的家具就是中国武汉的一位水泵工人阎明怡设计制造的，他平时就特别的喜欢制作迷你型的明式家具，已经保持这个爱好至少有20年的时间了，而就在1999年制造的一款微型明式家具被上海的吉尼斯世界纪录总部颁发了证书，而这些家具和实物几乎都拥有着一样的功能。...

发布时间：2024-04-10 20:00:16

世界上最无聊的三大发明:没有灵魂的自动撸猫器

世界上最无聊的三大发明分别是智能自动撸猫器、男士胸罩、Fliz自行车。其中智能自动撸猫器是最无聊的发明，据说是为了消解猫咪没有主人陪伴的焦虑心情，但是撸猫这种享受的事情也需要机器帮忙代劳是不是太过于无聊了。...

发布时间：2024-04-10 19:00:11

世界最累的工作排名:环卫工上榜第一危险系数超高

世界最累的工作排名分别是煤矿工人、建筑工人、环卫工、消防员、刑警、护士、菜农、巴士司机。其中煤矿工人是最累的工作，因为这项工作不仅是非常的脏和累，而且随时都存在生命危险，并且如果是小矿洞的话，那么工资也不会太高，只能勉强糊口。...

发布时间：2024-04-10 18:00:54

澳大利亚十大发明：原来有这么多影响世界的产品

澳大利亚十大发明分别是黑匣子、Wifi、谷歌地图、青霉素、人工耳蜗、冰箱、气胀式逃生滑梯、HPV疫苗、塑料镜片、超声扫描仪。这些发明几乎可以说都是对世界有着重大贡献的发明，其中黑匣子尤其能够在飞行事故中起到极大的作用，避免危险故事的在发生。...

发布时间：2024-04-10 17:00:18

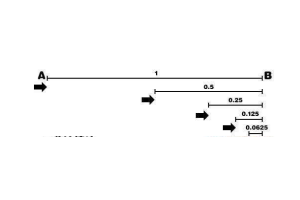
芝诺悖论是什么?古希腊飞人阿基里斯跑不过乌龟

古希腊哲学家芝诺其实提出了不少的悖论，其中最著名的四个分别是二分法悖论、阿基里斯悖论、飞矢不动悖论以及竞走悖论，这些悖论几乎都是想要争论世界上的时空到底是可分的还是不可分的，如果可分，那么第一和第三个悖论就无法解决，而如果空间是不可分的，则第三个无法解决。...

发布时间：2024-04-10 16:01:24

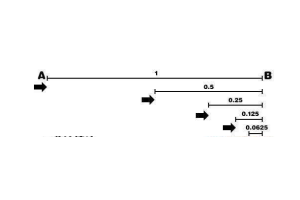
芝诺悖论是什么?古希腊飞人阿基里斯跑不过乌龟

发布时间：2024-04-10 16:01:04

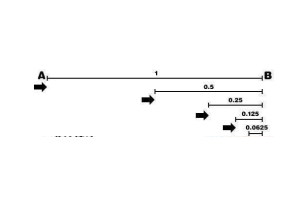
芝诺悖论是什么?古希腊飞人阿基里斯跑不过乌龟

发布时间：2024-04-10 16:00:55

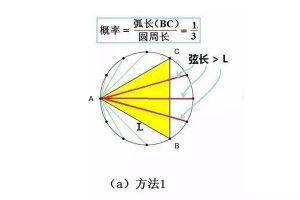
贝特朗悖论是什么?得出三种不同结果(但算法正确)

贝特朗曾经在1899年提出了一个悖论就是，假设一个内接圆的等边三角形中，任意选择一条弦，那么这条弦长于等边三角形边长的几率有多大?但结果却并不是唯一的，分别利用三种方法解答出了二分之一、三分之一和四分之一，可以说它们都完全正确但相互矛盾，因此就形成了一个悖论。...

发布时间：2024-04-10 16:00:06

上帝悖论逻辑上的漏洞:人类逻辑无法理解上帝

在宗教中几乎都是将上帝看作万能，但是曾经有人反驳“让上帝造一块自己无法拿起的石头吧”，这就是著名的上帝悖论，但其中也有不少人指出它是存在漏洞的，宗教主义者的说法是认为你不是上帝你怎么知道上帝无法造出，要知道蚂蚁也不知道莫比乌斯环是立体的，而无神论者则表示这只是一种反证法，假定上帝是万能的，于是就找出反例来验证上帝不是万能。...

发布时间：2024-04-10 15:00:19